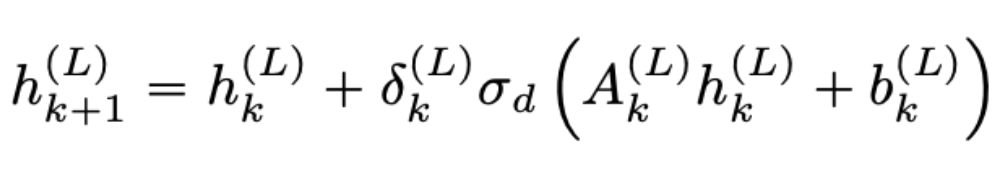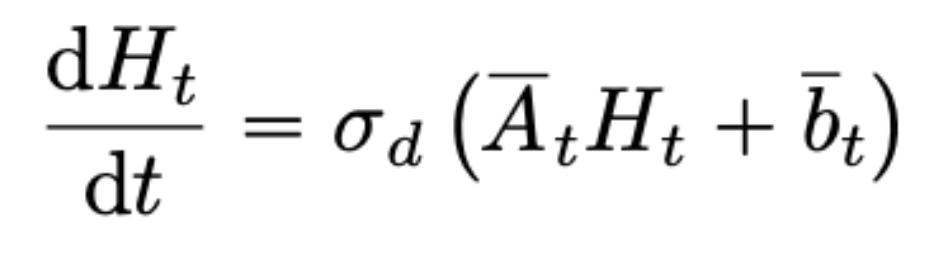Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have motivated the neural ordinary differential equations (neural ODE) architecture which garnered a lot of interest in the Machine Learning community. A widely established claim is that the Neural ODE is the limit of ResNets as the number of layers increases. A collaboration effort between InstaDeep and the University of Oxford challenges this claim by investigating the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. The conclusive research paper, the company’s first-ever submission to this conference, has been accepted to the renowned International Conference on Machine Learning (ICML) 2021 in the form of a short presentation at the event and for publication in the conference proceedings.
Significantly different scaling regimes
Our results show that ResNets do have a limit as the depth increases, however, we observe the existence of scaling regimes can be significantly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, or a stochastic differential equation (SDE), or neither of these.
These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.
Rockstar architecture
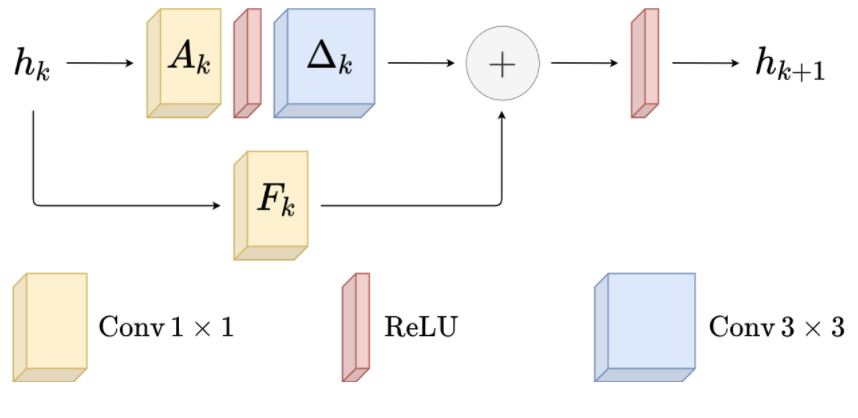
Let’s take a step back and look at the methodology behind the findings. ResNet is a favourite among Deep Learning architectures that has led to huge improvements for computer vision and speech recognition especially [1]. Below is a view of the architecture of a basic block of a residual network: it adds a convolutional transformation (\(A_k\) and \(\Delta_k\)) of the hidden state together with a skip connection \((F_k)\) of the same hidden state.
Stacking basic blocks together, we obtain below a generic representation of the residual neural network architecture for the CIFAR10 dataset. It takes as input a 3x32x32 tensor encoding an RGB image and outputs a vector in ten dimensions, where each dimension represents the probability that the image belongs to a given class.
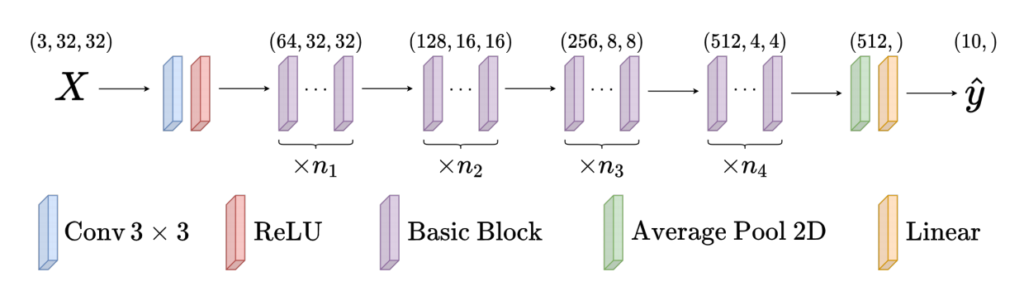
ResNet improved standard feedforward neural network architectures (FFNN) for the following reasons:
- Gradient vanishing/explosion: adding a residual (skip) connection helps stabilize the spectral norm of the gradient of the output with respect to the hidden states. Hence, we are able to go significantly deeper with ResNets than with FFNN (1000 layers vs. 30). As some problems require depth to improve accuracy, ResNets improve the state of the art on standardised datasets.
- Information theory: At initialisation, all the weights of the ResNet are close to 0 so the input-output map is close to the identity function, as opposed to the zero function for FFNN. Hence, we don’t lose any information at initialisation, and training will be about learning a more useful representation of the data. It is arguably easier than disentangling the feature space as the FFNN must do.
Introducing a general framework to encapsulate neural ODE assumptions and beyond
Over the years, researchers started to link ResNets to differential equations. They argue that a ResNet is in fact a numerical scheme of a given differential equation, which is a well-understood topic studied by mathematicians since Euler (1750) and which motivated new deep learning architectures [2]. This search culminated in the now-famous neural ODE model [3] that uses ODE schemes to train their model. We write below the (simplified) equations for the ResNet (left) and for the neural ODE (right).
To people familiar with differential equations, the link between the two equations only holds under particular conditions [4] that may not be satisfied in practice (see below). We may force these conditions at initialisation, but the weights trained with stochastic gradient descent (SGD) might not satisfy these conditions anymore.
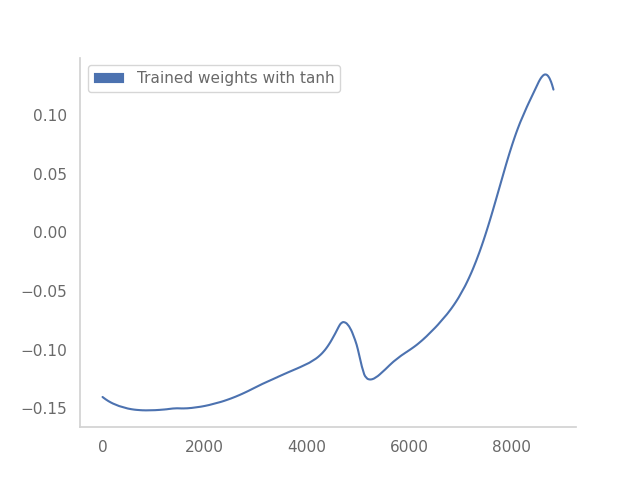
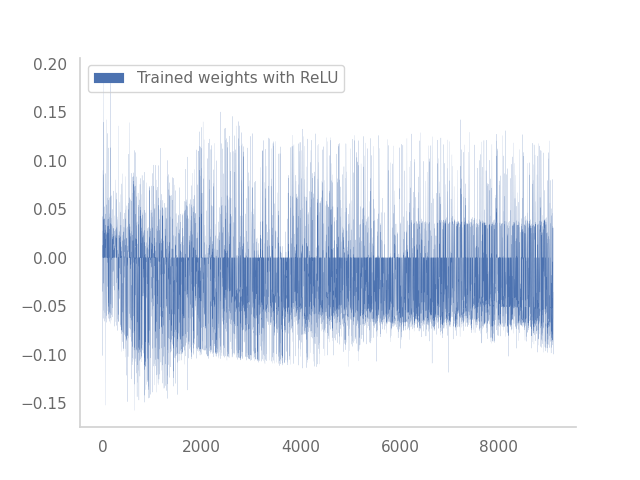
The main contribution of the paper is to introduce a more general framework for the trained weights of ResNets that encapsulates the neural ODE assumptions above, but also other cases. We test our hypothesis on synthetic and real-world datasets. We found that depending on the activation function, the shape of the trained weights for a very deep network (large L) looks drastically different. Let’s consider an example:
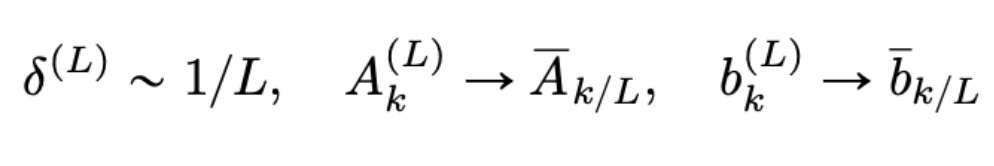
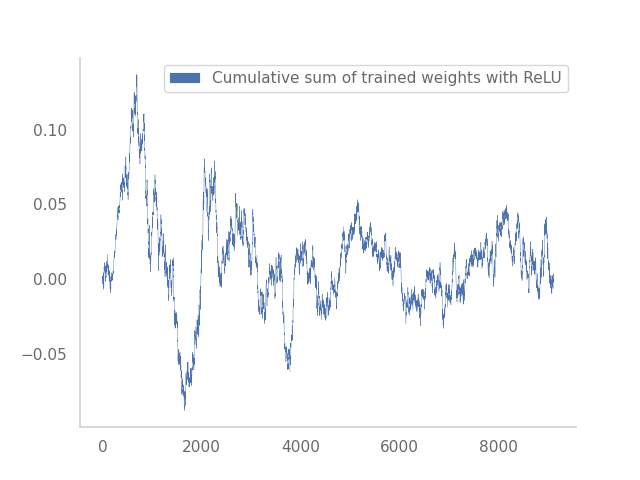
On the left, the non-linear activation of the ResNet is tanh, and on the right ReLU.
If you are not familiar with stochastic calculus, the plot on the right-hand side looks pretty much like white noise, i.e. the “derivative” of Brownian motion. We put derivative in quotation marks because Brownian motion is a rough function, so it can’t be differentiated in the traditional sense, but nonetheless has a derivative in the distributional sense. To “integrate” white noise, we shall take the running cumulative sum of the plot on the right-hand side. We get a process that now looks like a standard Brownian motion!
In the research paper, we lay down two general assumptions that describe the behaviour of trained weights of ResNets as observed above. We prove the convergence of their limiting equations, which can be either the neural ODE, a linear ODE or a linear-quadratic SDE (below).
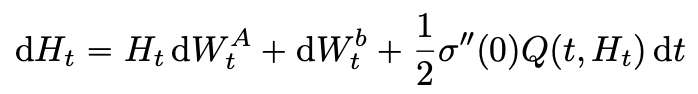
So what are the implications for practical training of ResNets? Knowing the scaling limit of trained weights will help you choose your initialization strategy. Also, training the limiting equation above in the neural ODE fashion will guarantee a good accuracy because of its clear connection with ResNets, and a reduced-form architecture with a low memory footprint.
Is this the end of the story? Of course not! Our results hold for fully connected networks, but we have observed that convolutional networks have a different scaling behaviour, such as a sparse limit. More on this to come so keep an eye on InstaDeep’s research space!
Research collaboration with University of Oxford
The ResNet paper is a result of close collaboration with InstaDeep’s research partner, University of Oxford. As a committed sponsor of Oxford’s Mathematics PhD programme, InstaDeep is currently supporting two PhD students with a scholarship. As part of their thesis, they both collaborate with InstaDeep’s R&D team on advanced research, such as this paper and others submitted to NeurIPS 2021. One of InstaDeep’s board members, Rama Cont, is also a Professor of Mathematics and Chair of Mathematical Finance at the University of Oxford.
As ICML is one of the three primary conferences in AI alongside NeurIPS and ICLR, this first acceptance to ICML is a true affirmation of InstaDeep’s boundary-pushing research initiatives. This year’s ICML is the thirty-eighth conference of its kind and runs from Sunday 18th July through to Saturday 24th as an online conference.
You can read the research paper in full on Arxiv.
The code for this paper can be found at https://github.com/instadeepai/scaling-resnets.
[1]: He, K., Zhang, X., Ren, S., and Sun, J. Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016.
[2]: E. Haber and L. Ruthotto, Stable architectures for deep neural networks, Inverse Problems, 34 (2018).
[3]: Chen, R. T. Q., Rubanova, Y., Bettencourt, J., and Duvenaud, D. K. Neural Ordinary Differential Equations. In Advances in Neural Information Processing Systems (NeurIPS) 31, 2018
[4]: Thorpe, M. and van Gennip, Y. Deep Limits of Residual Neural Networks, 2018.